X선회절 (X-Ray Diffraction, XRD)

1.X선회절현상 이란 ? (X-Ray Diffraction, XRD)

X선 회절(X-Ray Diffraction, XRD)은 물질의 내부 미세구조를 밝히는데 매우 유용한 수단이다.

X선(X-Rays)이 발견되기 전에 이미 빛의 회절(Diffraction)은 잘 알려져 있었으며, 만일 결정이 일정한 간격으로 규칙적인 배열을 한 원자로 되어 있고, 또 X선(X-Rays)이 결정내의 원자사이의 거리와 거의 비슷한 파장을 가진 전자파라면, X선(X-Rays)이 결정에 의해서 회절(Diffraction)될 것이라고 추정하였고, 이것을 실험적으로 성공한 것은 1912년 독일의 von Laue 에 의해서 였다.
다음 사진은 결정에 X선(X-Rays)을 조사 시켜서 회절된 X선(Diffracted X-Rays)에 의하여 film을 감광시킨 사진으로, 작고 검은 반점들이 X선(X-Rays)이 검출된 위치다.

Laue의 반점

이것은 X선(X-Rays)의 파동성과 결정내 원자의 규칙적인 배열을 동시에 입증한 계기가 되기도 하였다.

같은해 영국의 W.H. Bragg는 이를 다른 각도로 해석하여 Laue가 사용했던 수식보다 더욱 간단한 수식으로 회절에 필요한 조건을 Bragg's law (2 d Sin q = n l) 로 나타내었으며, 이 X선회절현상(X-Ray Diffraction)을 이용하여 각종물질의 결정구조를 밝히는데 성공하였다.

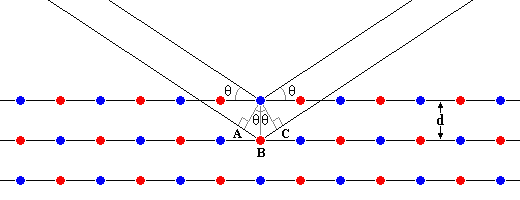
두개 이상의 파동 사이에 서로 위상차이가 그 파동의 반파장 만큼 있을때는 서로 상쇄되어 파동이 사라지나, 위상차이가 파장의 정수배 만큼 있을때는 진폭이 두배로 되어서 세기가 더 크게된다.

다음 그림에서 A에서 B까지의 거리는 d Sin q 가 되며, 이는 B에서 C까지의 거리와도 같다.
따라서, AB = BC = d Sin q 이며, n l = 2 d Sin q 를 만족하면 X선(X-Rays)은 회절(Diffraction)되어 강하게 나타나게 된다.

AB = BC = d Sin q n l = 2 d Sin q

이 X선회절현상(X-Ray Diffraction)을 이용한 X선 회절 분석법(X-Ray Diffractometry)은 초기에 비교적 단순한 형태의 결정 물질속에 있는 원자들의 배열과 상호거리에 관한 지식과 금속, 중합물질 그리고 다른 고체들의 물리적 성질을 명확하게 이해하는데 많은 도움을 주었다.

최근의 X선회절(X-Ray Diffraction) 연구는 Steroid, 비타민, 항생물질과 같은 복잡한 자연물의 구조를 밝히는데 주로 이용되고 있다.
또한, 임의 시료가 어떠한 성분으로 구성되어 있는지 몰라도, 이 시료에 X선(X-Rays)을 조사시켜서 나타나는 회절패턴(X-Ray Diffraction Pattern)을 이미 알고있는 시료에서 얻어진 회절패턴(X-Ray Diffraction Pattern)과 서로 비교하여 그 성분을 알아낼 수 있다.

2. 결정에 의한 회절(Diffraction)

물질에 입사된 X선(X-Rays)의 일부는 파장이 변화없이 산란한다.(간섭성 산란, Thomson 산란)
이 산란은 한개 한개의 전자에 의하여 생긴다.
원자는 전자의 집합체로 이루어져 있으므로, Thomson 산란과 같은 간섭은 원자에 의한 X선(X-Rays)의 산란으로 증명된다.
원자가 규칙적으로 배열되어 있는 결정체는 원자에 의한 산란X선(Scattered X-Rays)의 간섭결과로 특정방향으로 강하게 산란한다.

다이아몬드의 구조

ZnS(섬아연광)의 구조

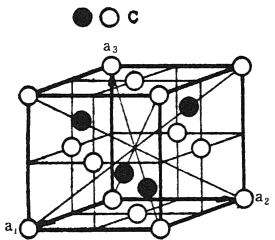
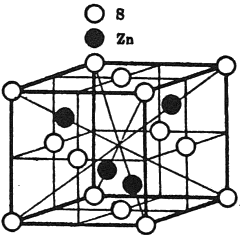
1) 전자에 의한 X선의 산란(X-Ray Scattering)

다음 그림과 같이 임의의 전장 Vector E 와, 1차X선(Primary X-Rays)의 입사방향을 0 -> y 라 하고, 그 전장 Vector 의 x축, z축 방향의 성분을 각각 E_x, E_z 라고 할때, 원점 0 에 있는 한개의 전자에 의한 X선산란(X-Ray Scattering)을 보자.

전자에 의한 X선의 산란(X-Ray Scattering)

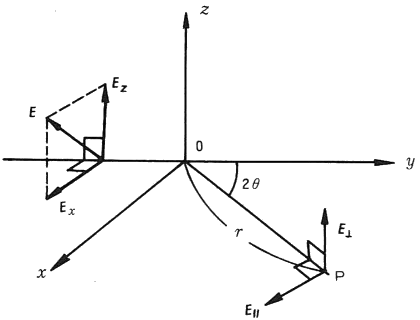
x,y 평면내에 0y 와 2q의 각도, 0 에서 거리 r 의 관측점 P 에서 전자의 산란에 의한 전장 E₀ 을 보면

X선관(X-Ray Tube)에서 나오는 X선(X-Ray)은 그 전장의 진동이 방향성을 가지고 있지 않으므로,

와 같은 관계가 성립한다.

다음에 X선의 강도(X-Rays Intensity) I₀는 비례상수를 k 라 할때

전자에 의한 산란X선강도(Scattered X-Rays Intensity) I_e를 구하면

가 된다.
이 식을 Thomson 산란(Thomson scattering)의 식이라 한다.

2) 원자에 의한 X선의 산란(X-Ray Scattering)

원자에 의한 X선의 산란(X-Ray Scattering)을 원자번호 Z의 원자에 대하여 보면, Ze의 전하를 가지고 있는 원자핵과 Z개의 전자에 의한 산란이 있으므로, 원자핵에 의한 산란은 전자에 의한것에 비하면, 1/2000 정도로 무시할 수 있으므로 궤도전자에 의한 산란만을 본다.

원자에 의한 X선의 산란

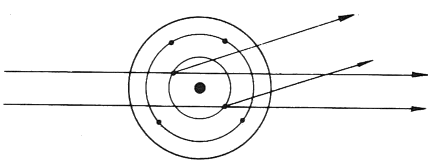
입사 X선(Incident X-Rays)과 동일한방향의 산란은 전자 한개에 의한 산란의 Z배가 되나, 입사 X선(Incident X-Rays)방향과 각도를 갖고있는 방향은 각각의 전자에 의한 산란X선과의 사이에는 간섭하여 감소하는 경향이 있다.

원자 산란 Factor

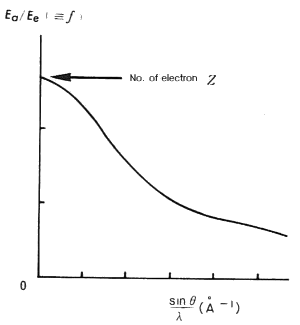
전자의 분포밀도를 r(r)라 하고, 원자에 의한 산란X선(Scattered X-Rays)의 전장Vector(Electric field vector) E_a는 다음과 같다.

Ea = Ee

r(r) exp{2pi/l r( S - S0)} dv

Ea	: 원자에 의한 산란X선(Scattered X-Rays)의 전장 vector
Ee	: 한개의 전자에 의한 산란X선(Scattered X-Rays)의 전장 vector
r(r)	: 전자밀도분포
l	: X선(X-Rays)의 파장
r	: 전자의 좌표
S0	: 입사X선(Incident X-Rays)의 방향의 단위 vector
S	: 산란X선(Scattered X-Rays)의 방향의 단위 vector

원자산란 factor(Atomic scattering factor) f 를 다음과 같이 정의하면,

f =

r(r) exp{2pi/l r( S - S0)} dv

E_a 는 다음과 같다.

3) 결정에 의한 회절현상(Diffraction)

결정에 X선(X-Rays)을 조사하면 결정중의 각각의 원자에 의하여 산란된 X선(X-Rays)이 서로 더해지며, X선(X-Rays)이 단색일 경우 각각의 원자에 의해 산란된 X선(Scattered X-Rays)이 서로 간섭하여 특정방향에 강한 회절X선(Diffracted X-Rays)이 생긴다.

결정에 의한 산란

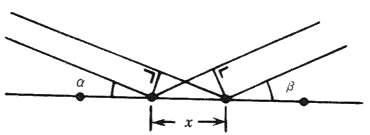
X선(X-Rays)이 a각도로 입사되어 b각도로 산란될때, 표면상에 x 만큼 떨어진 2점에서의 X선(X-Rays)의 경로차는

가 되며,
행로차가 파장의 정수배 nl와 같은경우 강해지며, 표면상에서의 산란X선(Scattered X-Rays)이 동일위상이 되려면 nl=0가 되며, a=b가 얻어진다.
따라서 한층의 표면에서 최대 강도를 얻을 수 있는 간섭현상은 입사각과 산란각이 같을 때이다.

Bragg's 회절조건

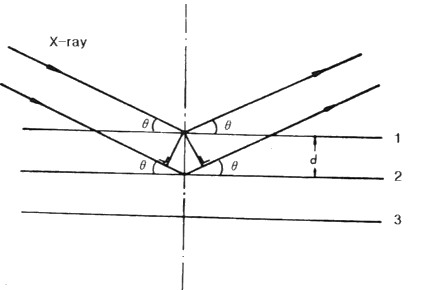
다수의 격자면 으로부터의 산란X선의 간섭을 보면, 제1면과 제2면과의 X선간섭에는 제1면과 제2면의 간격에 의한 행로차 만이 문제된다.
제1면과 제3면 그외에 다른 평행면의 간섭도 똑같이 면간격에 의한 행로차 만이 문제된다.

제1면과 제2면의 행로차는 2d sin q 가 되며, 파장의 정수배의 경우 강하게 된다.

이 식을 Bragg의 공식(Bragg's formula)이라고 한다.

3. 역격자와 회절(Diffraction)조건

입사X선(Incident X-Rays)의 조사영역 안에 2가지 이상의 결정입자가 존재하는 다결정체 에서는 일반적으로 다수의 결정입자가 여러방향으로 향하고 있으므로, 시료에 조사되는 X선(Incident X-Rays)의 방향은 문제가 되지 않는다.
그렇지만, 입사X선(Incident X-Rays)의 조사영역 안에 단일 결정이 존재하는 경우에는 입사X선(Incident X-Rays)의 방향과 결정의 방향과의 관계는 회절X선(Diffracted X-Rays)을 발생시키는 중요한 조건이 된다.

역격자와 역격자점

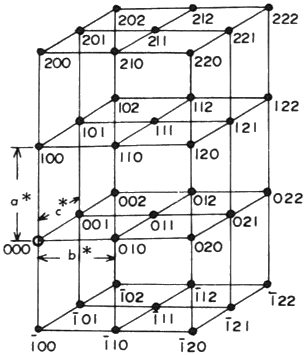
결정격자에 의한 X선의 회절(X-Ray Diffraction)현상을 쉽게 이해하기 위하여 역격자(reciprocal lattice)의 개념을 도입해 보자.
이것은 1921년 Ewald가 유도한것으로 처음에는 추상적이고 부자연스럽게 생각되었으나 지금은 X선 회절(X-Ray Diffraction)현상을 이해 하는데 불가결한 것이 되었다.

결정은 원자의 집단으로 구성되어 있으며 복잡하게 되어 있지만, 일정한 주기로 3차원적으로 반복적으로 구성되어 있다.
이 주기적 단위의 크기는 격자정수로 나타내며, 여기서 격자정수를 3개의 기본 vector a, b, c로 표시한다.
그 크기는 |a| = a₀, |b| = b₀, |c| = c₀ 이며, b와c, c와a, a와b의 사이의 각도를 각각 a, b, g 라고 한다.

이 3개의 기본 vector로 표시된 기본격자에 대하여 다음과 같은 기본 vector a^*, b^*, c^* 를 정의한다.
V 를 단위격자의 부피라고 하면,

가 되며, 이 a^*, b^*, c^* 를 역격자 기본 vector(reciprocal lattice vector)라 하며, a^*, b^*, c^*, a^*, b^*, g^*를 역격자정수(reciprocal lattice constant)라 한다.

단색화된 파장 l의 X선(X-Rays)이 다음 그림의 O(역격자 원점)를 향하여 입사되고, O 에서 1/l 만큼 떨어진 A 를 중심으로 반경 1/l인 구상에 H 가 있을때, 입사된 X선이 A 에있는 시료에 의해 회절되어 H 를 향하여 발생되면

반사구와 회절(Diffraction)조건

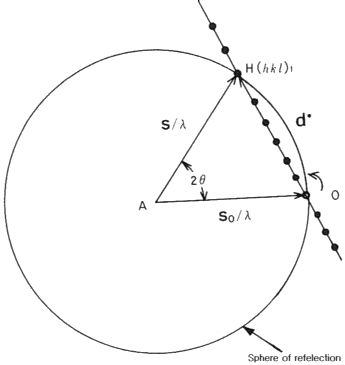
S₀를 입사 방향의 단위 vector, S를 회절(Diffraction)방향의 단위 vector 라고 하면,

이 되며, | S - S₀ | = 2 sin q 이므로,

가 된다.

이 구를 Ewald의 반사구(sphere of reflection)라고 한다.